egbert@coas.oregonstate.edu

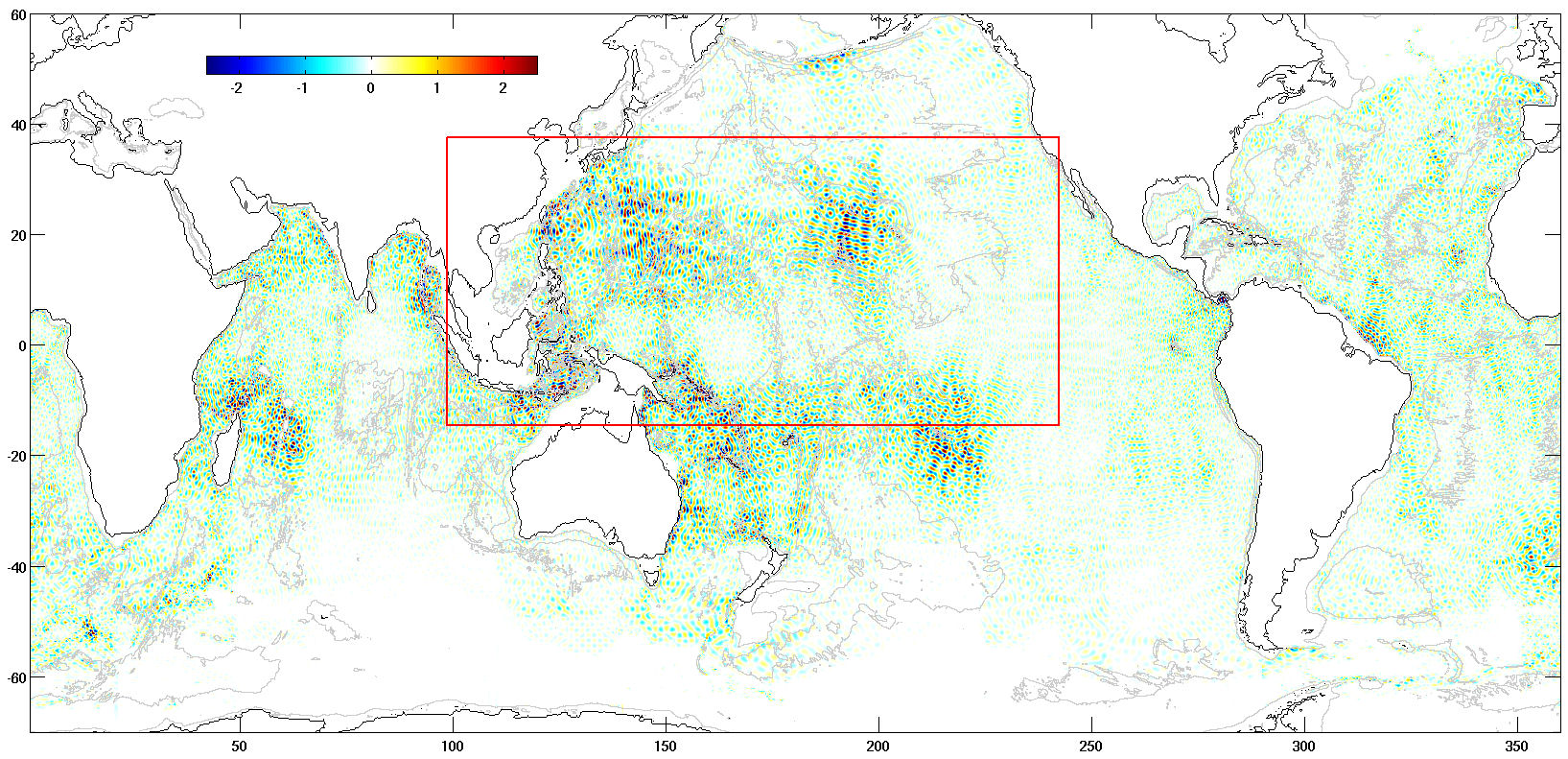
M2 1st mode Internal Tide Map (in-phase, cm)
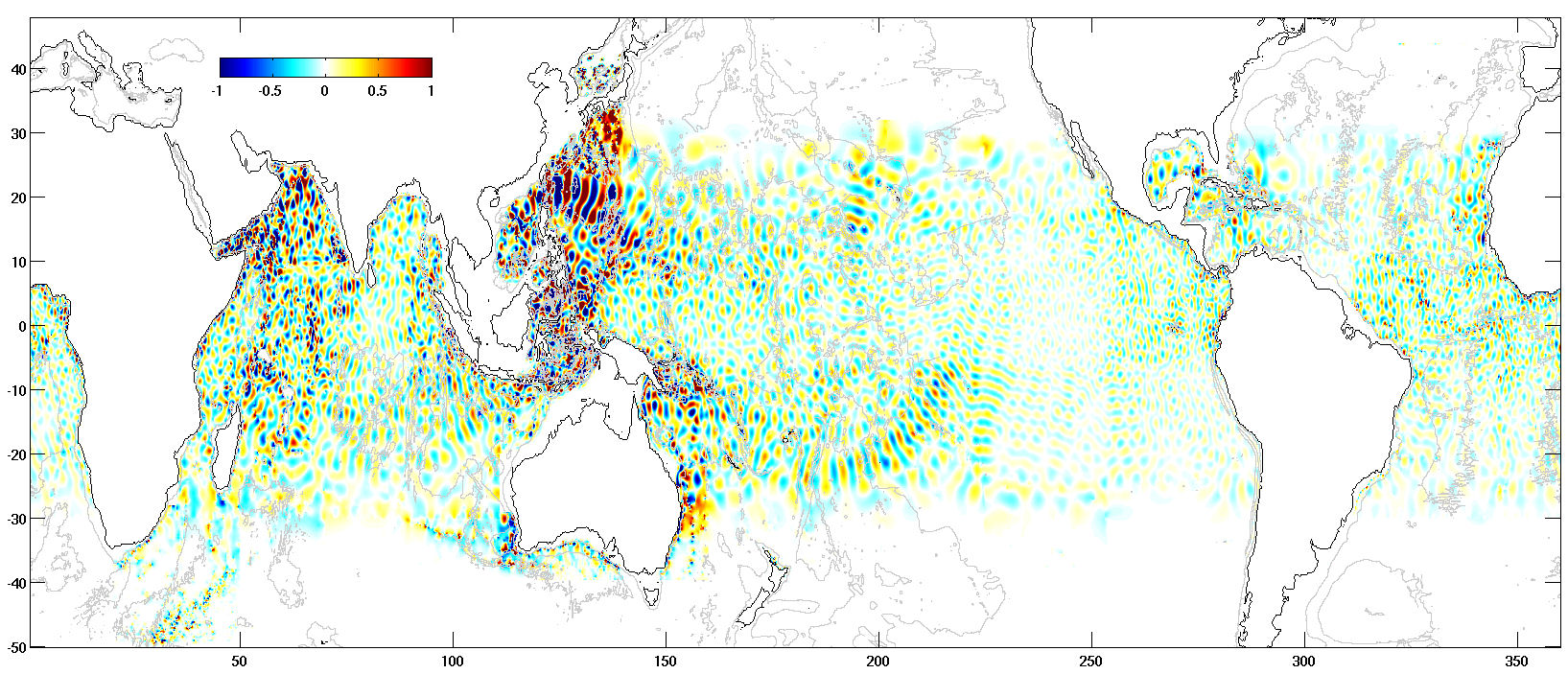
K1 1st mode Internal Tide Map (in-phase, cm)
We have developed a reduced gravity (RG) data assimilation scheme for mapping
low-mode coherent internal tides [Egbert and Erofeeva (2014)],
and applied this to a multi-mission dataset to produce preliminary global
first-mode M2 and K1 solutions. Our scheme is based on the
Boussinesq linear equations for flow over arbitrary topography with
a free surface and horizontally uniform stratification. As in [
Tailleux and McWillims (2001)] and [
Griffithsand Grimshaw (2007) ] vertical dependence of
the flow variables are described using flat-bottom modes (which depend
on the local depth H(x, y)),
yielding a coupled system of (2-dimensional) PDEs for the modal
coefficients for surface elevation and horizontal velocity.
Equations for each mode are coupled through
interaction coefficients, which can be given in terms of the vertical mode
eigenvalues following the approach of [
Griffithsand Grimshaw (2007) ]. Modes are decoupled wherever bathymetric gradients are zero,
and for a flat bottom the system reduces to the usual single mode
RG shallow water equations.
For our RG scheme we drop the vertical-mode coupling
terms to obtain independent equations for the propagation of
each mode with spatially variable reduced water depth,
which we determine from local bathymetry and stratification. These
simplified equations are
identical to the linear SWE used in OTIS, allowing us to
thus use the assimilation system to map internal
tides by simply modifying depth, and fitting along-track harmonic
constants as a sum over a small number of modes.
With some extensions to OTIS, coupling terms for
the first few modes can be included in the dynamics.
We have applied the OTIS-RG assimilation scheme to construct global maps
of first mode temporally coherent internal tide elevations.
All available exact repeat mission data were assimilated
(TP/Jason, ERS/Envisat), with the AVISO weekly gridded SSH product used
to reduce mesoscale variations before harmonic analysis.
Solutions are computed in overlapping patches (~ 20 x 30
degrees), and then merged (via weighted average on overlaps) into a
global solution. We note that
adjacent solutions almost always match quite well even without this
explicit tapering. Elevations for the intitial RG assimilation
solutions are shown for M2 and K1, first mode.
!!! NOTE: these internal tide solutions are prliminary, and are not available for download !!! !!!